
OT図とは、2つの量の積が第3の量になる関係を表現する暗記の手段で、第3の量を表す記号を上段に配し、その他の量の記号を下段に配する図表を総称していう。日本では円を三分割しあたかもOの中に Tをはめこんだ枠組みの中に3つの量が書き込まれることから、OT図と呼ぶことにしたが、海外の事例、例えば三角形を三分割した図表、上下を割線で区切ったもの、上下を分ける記号をもたないものも含めてOT図と呼ぼう。
OT図の起源は、オームの法則に登場する3つの量、電流、電圧、抵抗の関係をこの図に表したものである。ニューヨークの電気専門の週刊誌 The Electrical World の 1892年6月25日号にA Practical Form of Ohm's Lawという挿絵付きの記事が載った。 無署名のこの記事は、電気関係の実務者であってもオームの法則を間違えやすいこと、エジソン電気照明会社勤務のハーバート・M・ピルキントンがEを上段に、CとRを下段に配する意匠を作成したことを伝える。挿絵のとおり、ピルキントンの意匠では 上段のEはCとRに比べ2倍程度の大きさを持っている。The Electrical Worldはこれをバッジにすればどこにいても利用できると提案している。以下がその全文である。
An ingenious little device has been got up by Mr. Herbert M. Pilkington, of the Edison Electric Illuminating Company, of Brooklyn, which is shown in the accompanying illustration. Every one who has had anything to do with the application of electrical laws has no doubt found it difficult at times to remember even so simple a one as that of Ohm. Of course every one knows Ohm's law, but somehow just at the moment when it is most needed it manages to get twisted around into a state of hopeless confusion. This device is intended as a remedy for all these troubles and to make the application of the law a matter of the utmost simplicity. The design may be worked up into an appropriate badge that can be worn where it is always at hand. By merely placing the finger over R one finds C E staring him in the face. Or if E is covered value C R is plainly seen. Concealing C will bring E R boldly out.

ピルキントンの提唱したOT図は直ちに各国に伝播した。ロンドンの専門週刊誌 The Electrician は 1892年7月8日号にこの記事をほぼそのまま転載している。 同誌の独自性は E C R のようにEとC Rを同じ大きさで示し、Eを下段の2文字の中間の上方に配したことと、この意匠をバッジにするのではなく単に2フィート定規に彫り込めばよいとからかいを含んだ提案をしたことである。
さらに2週間後、パリの専門隔週誌 L'Industrie Électrique が 1892年7月25日号でピルキントンのOT図を報じた。この記事は無署名だが、 続く記事がThe Electrician誌の内容を引き、同じような海外事情紹介になっていることと、その記事にG. R.が署名していることから、もしかすると同一人物の記事かもしれない。G. R.は編集次長(secrétaire de la rédaction)の G・ルー (G. Roux)と思われる。ルーはパリ市物理工業化学学校の応用電気学主任(chef des travaux pratiques d'électricité à l'École de physique et de chimie industrielles de la Ville de Paris)でもあった。
さてこの記事は、代数を心得ない者にはオームの法則を表す最頻出の式の形を変形して任意の量を計算することが難しいと述べ、ピルキントンのOT図がこの障害を取り払ったことを歓迎している。電流をフランスの習慣に合わせて、英語圏の C から I に直した以外は、The Electrician 誌のOT図の体裁をほぼ踏襲している。すなわち、 E R I に囲み枠を施したものを提示している。ここでさらに電圧を E ではなく V で表すと、現代日本で使われるオームの法則のOT図になる。
記事は次に、キャパシタに蓄積される電気量が電圧と静電容量の積で表される関係を表す独自のOT図を提唱している。Q = C E という公式の基本的な形を自由に変形できない初心者の便宜を図ったと述べている。電気量の公式を表す Q C E は、OT図が初めて変異した例と思われる。ピルキントンの原図が記事になってからわずか一ヶ月後のことである。19世紀末の情報伝達の速さに驚くばかりでなく、OT図の生産性にも注意すべきであろう。

日本でも遅くても戦時中から、オームの法則を表すOT図が存在する。武田 (1943: 9)は、 青少年を対象とした参考書の中で、電圧、電流、抵抗をOT図に書き入れた例である。
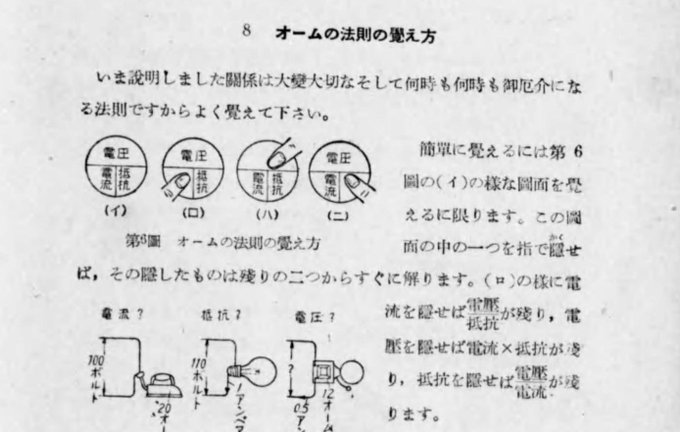
山口大学教育学部で永年、理科教育を講じた堂面春雄(1930年生、2014年歿)は、 堂面 (1988: 72) で【この手法は古くから流布しているようで、筆者も旧制中学校在学中に耳目にした。】と述べている。武田 (1943)と同時期に 学校生活の中でオームの法則のOT図にふれたという証言とみなせる。
戦後最初期にはすでに小学校の理科教育関係者の著作にオームの法則のOT図が確認される。『電気の科学』の著者実野恒久は第1版の1947年には大阪第一師範学校教官で、第2版の1958年には科学技術教育研究所に所属していた。 実野の著作は内容からして、武田の著作より対象年齢が低いものと思われる。実野は、実野 (1982) の奥付けによれば【昭和22年以来、小学校理科教科書(啓林館)の執筆・編集】に従事していた。以下の画像は 実野 (1947: 309) と実野他 (1958: 206) から。第2版の描き手は広瀬賜寿夫または坂口巌である。
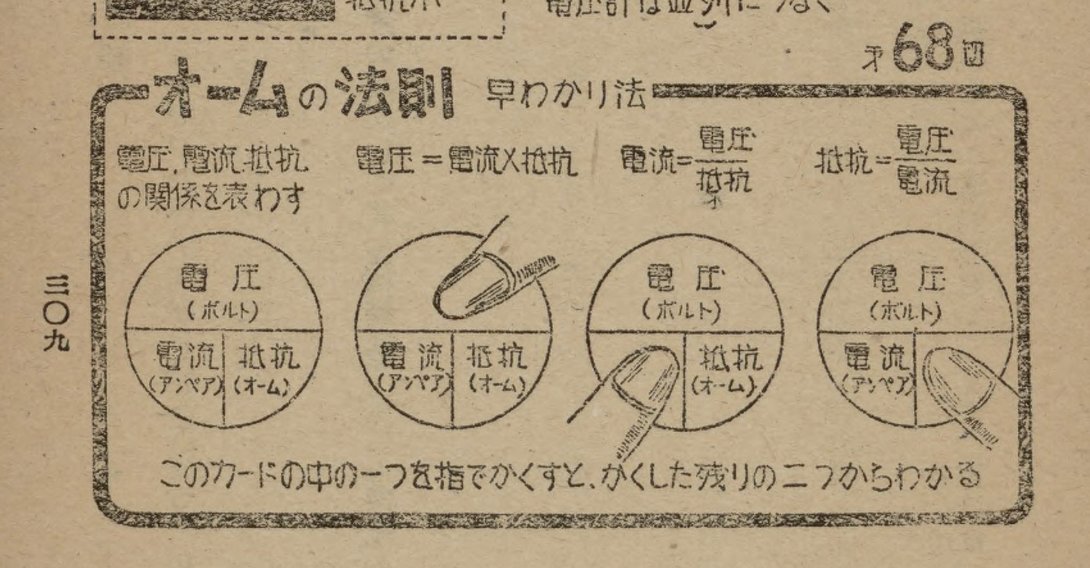
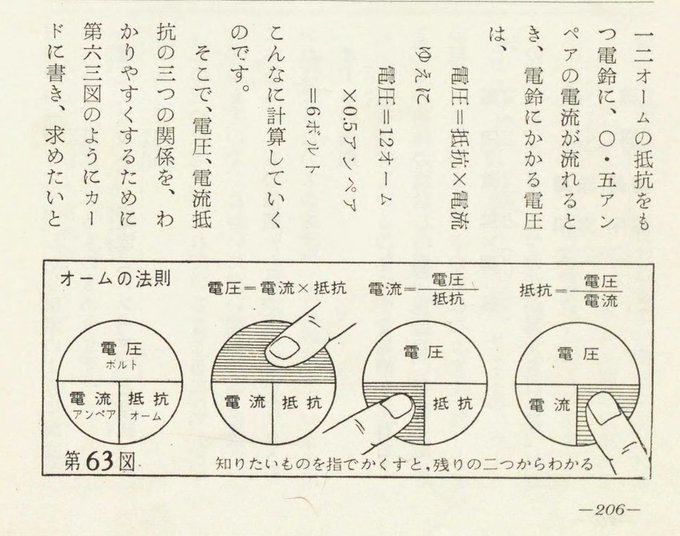
1960年代には、中学生がOT図を提案するという現象が確認される。旺文社発行の月刊誌『中学時代』(1960年11月号)の132ページには「頭によくのこる暗記法」というコラムがあり、学習事項の覚え方を読者が投稿したものを編集部が掲載している。 この雑誌の接頭副題は「高校受験」。読者は中学生である。この号では理科に関する覚え方の中にオームの法則のOT図が2人の中学生によって提案されている。【またこれと同じような方法で、数学の比例反比例の公式を求めることもできます。】ともあり、 正比例のOT図と反比例のOT図も掲載されている。投稿者のいずれかによるものか編集部の加筆なのか定かでないが、早くも60年に、正比例、反比例の関係にある他の数式もOT図で表せるとの示唆がなされたことは記憶されるべきである。
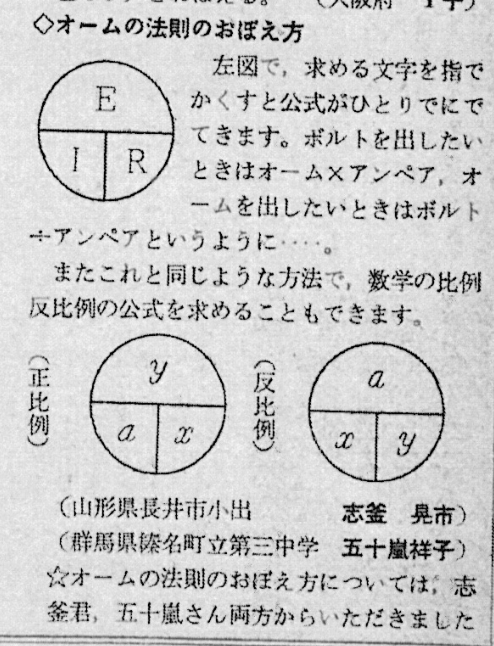
旺文社のこの雑誌は学年別に分割された後も暗記法の読者投稿を掲載した。『中三時代』 1964年11月号には「これは名案: 勉強法のグッド・アイディア」という読者投稿欄があり(162,3ページ)、「公式の覚え方・使い方」という項で終わっている。 他の項は投稿者の住所氏名があるがこの項にはなく、編集部の筆になる可能性が高い。そこでは、音の速さ = 波長 × 振動数の関係が【オームの法則の覚え方と同じように】OT図で書き表せることが紹介され、【そのほかにも、このような図が使える公式】 の例として、光度 = 照度 × [距離]²が挙げられていた(163ページ)。オームの法則のOT図が完全に常識化している前提で、他の量同士の関係にもOT図を利用させる狙いがあったと思われる。

70年代には、OT図を中学校の数学の授業で指導したという報告が現れる。中村恵一(1977: 62)は【落ちこぼれの問題が大きくとりあげられるようになってから、分る授業ということが、大きな研究課題となった】時代の要請に応えて 【絵と作表による文章題の解き方の指導は…分る授業でしかも考えさせる授業が実施できる試み】をなしたと研究の意義を述べる。
アメリカで1979年1月ティーハンが割合のOT図を提案したのとほぼ同じ頃、日本では速さのOT図が指導されていた形跡がある。 はにわ好き氏は、SNSおよび 私信(2024年7月18日)で、日本の小学校で1979年度に速さの授業でOT図を指導されたと証言している。速さの単元で、先生は初め、一般的な方法で指導していたが、ある授業でわからない児童はこの図を描いて当てはめるようにと、 三分割された円の中に道のり・速さ・時間と書き込んだOT図を示したという。はにわ好き氏は、単元テストで答えがあっていたのにOT図を描かなかったという理由でバツをつけられたことを克明に記憶していた。
80年代には、ひらがな3文字の略称をもつOT図の存在が確認される。尚、上の中村、秋山両者の論文を再録する大部の実践集が公刊されたのもこの時代である。
オームの法則のOT図も依然みられる。上述の堂面の述懐は、堂面 (1988: 72)が【中学校教師用書の例 (禿ほか1984)】に【オーム則の「暗記法」】を見出した際のものである。堂面 (1988: 85)の【参考文献】は、 この指導書を【禿 宗男ほか1984。改訂中学校理科・1分野下・教師用指導書。大日本図書刊。】と記している。ただし堂面 (1988: 73)はOT図に批判的で、【しかし「オーム則」は本来丸暗記すべき事柄ではない。 「単なる公式として暗記し、これに当てはめて問題を解く」訓練を重ねてきたと思われる諸君が、この記憶を失ったとき無惨な敗北を喫して 当然といえる。 「オーム則」では、その本質を理解していれば、記憶の必要は全く無い…。】と述べている。当時行われた三角関数の暗記ものを【正・余弦・正接を「水車 (垂/斜)、停車(底/斜)、水底 (垂/底)に横たわる」と暗記する法が知られている】(同)と 肯定しているのと対照的である。1984年に教師用指導書という半公式的な文書にOT図が掲載されたことは、OT図が学校教育に浸透し始めた初期の例として重要である。
2024年時点で現用の大日本図書の中学理科教科書に付属する教師用指導書も、オームの法則を表すOT図を掲載している。大日本図書編 (2021: 182)のレプリカを提示しよう。このページは「単元3 電流とその利用」に含まれ、 レプリカは指導書の下段注になっている。
◉中学校1年で学んだ密度の計算同様、生徒はわり算を敬遠しがちだが、繰り返し練習問題をさせて、数値の扱いに慣れさせる。
◉オームの法則の式は、小学校5年で学習した道のり・時間・速さの関係式に似ており、2つの数値から残りの1つの数値を計算で求められる。
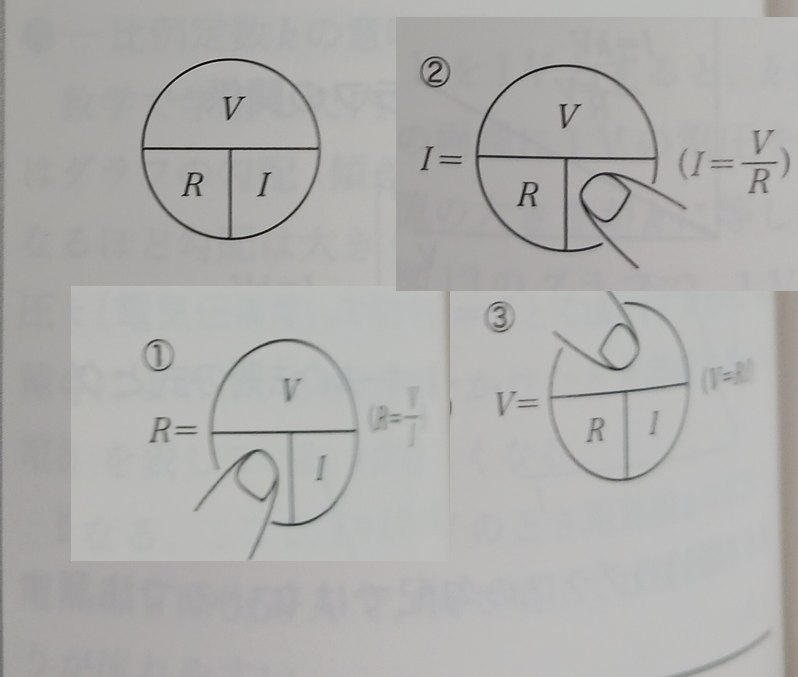
当時、学校教育の外でもOT図は、禿宗男他 (1984: 67)にデザインが近いものが流布していた。